Нулевое разглашение можно применять не только для абстрактных или непонятных вещей. Данный пример может быть немного неординарным для протоколов нулевого разглашения, но всё же он имеет место.
Представим себе некоего телекоммуникационного магната с огромными финансовыми возможностями, который хочет создать новую сотовую сеть. Сетевую структура сети можно посмотреть на рисунке ниже. Каждая верхушка представляет из себя сотовый трансмиттер, линии соединения или грани это точки пересечения двух сот. В данных местах трансмиттеры создают помехи, влияющие друг на дружку и мешают работать сети в целом. Для исключения этих помех каждую вершину можно настроить на один из трёх возможных частотных диапазонов.
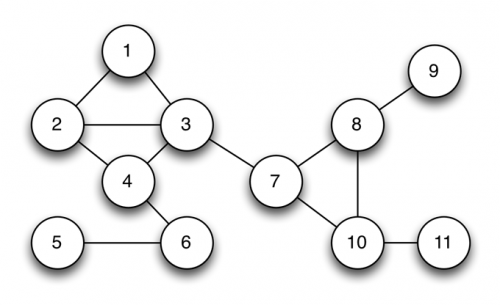
Следовательно, для того чтобы запустить такую сеть необходимо решение вопросов назначения своей полосы пропускания каждой вершиной с целью исключения пересечения клеток. Чтобы это изобразить наглядно необходимо использование разных цветов на нашем рисунке. Каждый цвет будет символизировать свою частотную полосу в нашей сети. Тогда результат будет таким, как на рисунке ниже.

Как многие поняли, наш пример это частная вариация всем известной теоретической сложности. Пример имеет название - проблема окраски графа в 3 цвета. Возможно вам даже известна отличительная особенность этого интересного вопроса. В некоторых случаях нахождение решения для каждого графа может быть затруднено, а иногда невозможно даже узнать существует ли вообще какое либо решение. Задачи окрасок графов и поиск решений к ним имеют название NP-полные задачи.
Конечно в приведённом нами примере решение можно получить очень просто в силу лёгкости задачи. А что же происходит когда задачи намного сложнее. К примеру, можно вернутся к нашей начальной задаче, но представить что сеть очень сложная, большая и разветвлённая. Эта сеть настолько сложна, что вычислительной мощности моих ресурсов просто бы не хватило для получения решения этой задачи. Вот здесь то мне и понадобились бы другие ресурсы, которым эта задача по плечу, чтобы я мог перенаправить им решение моей задачи. Можно было бы воспользоваться ресурсами какой нибудь большой корпорации с невероятными вычислительными мощностями.
Но тут всплывает один нюанс. Даже если мне удастся заручится поддержкой вычислительной мощности крупной корпорации, чтобы окрасить все мои графы, я не буду платить им до тех пор, пока не буду уверен в том, что у них действительно есть моё решение. А вот корпорация поведёт себя аналогичным образом и не будет передавать мне решение пока я не заплачу за него. То есть мы оба окажемся в тупиковой ситуации.
В реальности конечно можно найти выход из этого положения просто пригласив к сделке юристов и эксроу-посредников. Но мы ведь обсуждаем не реальную сферу, а криптографию. А как говорят сами криптографы в своих работах, для того, чтобы найти решение какого либо вопроса, нужно просто придумать полностью выходящее за рамки установленных норм решение. То есть это должно быть неординарное техническое решение.
Для получения такого решения корпорация пошла на консультацию к специалисту Силвио Микали, сотруднику MIT. Он посоветовался со своими хорошими коллегами Оде Голдрихом и Ави Виджерсоном. В результате этих переговоров был разработан новый протокол, который оказался настолько передовым, что для его функционирования даже не нужны компьютеры. Всё оказалось очень просто. Нужно просто большое количество разноцветных карандашей и бумажные листы. К тому же понадобится приличное количество шляп. А вот насколько просто и как это будет всё работать, рассмотрим в следующей статье.
Представим себе некоего телекоммуникационного магната с огромными финансовыми возможностями, который хочет создать новую сотовую сеть. Сетевую структура сети можно посмотреть на рисунке ниже. Каждая верхушка представляет из себя сотовый трансмиттер, линии соединения или грани это точки пересечения двух сот. В данных местах трансмиттеры создают помехи, влияющие друг на дружку и мешают работать сети в целом. Для исключения этих помех каждую вершину можно настроить на один из трёх возможных частотных диапазонов.

Следовательно, для того чтобы запустить такую сеть необходимо решение вопросов назначения своей полосы пропускания каждой вершиной с целью исключения пересечения клеток. Чтобы это изобразить наглядно необходимо использование разных цветов на нашем рисунке. Каждый цвет будет символизировать свою частотную полосу в нашей сети. Тогда результат будет таким, как на рисунке ниже.

Как многие поняли, наш пример это частная вариация всем известной теоретической сложности. Пример имеет название - проблема окраски графа в 3 цвета. Возможно вам даже известна отличительная особенность этого интересного вопроса. В некоторых случаях нахождение решения для каждого графа может быть затруднено, а иногда невозможно даже узнать существует ли вообще какое либо решение. Задачи окрасок графов и поиск решений к ним имеют название NP-полные задачи.
Конечно в приведённом нами примере решение можно получить очень просто в силу лёгкости задачи. А что же происходит когда задачи намного сложнее. К примеру, можно вернутся к нашей начальной задаче, но представить что сеть очень сложная, большая и разветвлённая. Эта сеть настолько сложна, что вычислительной мощности моих ресурсов просто бы не хватило для получения решения этой задачи. Вот здесь то мне и понадобились бы другие ресурсы, которым эта задача по плечу, чтобы я мог перенаправить им решение моей задачи. Можно было бы воспользоваться ресурсами какой нибудь большой корпорации с невероятными вычислительными мощностями.
Но тут всплывает один нюанс. Даже если мне удастся заручится поддержкой вычислительной мощности крупной корпорации, чтобы окрасить все мои графы, я не буду платить им до тех пор, пока не буду уверен в том, что у них действительно есть моё решение. А вот корпорация поведёт себя аналогичным образом и не будет передавать мне решение пока я не заплачу за него. То есть мы оба окажемся в тупиковой ситуации.
В реальности конечно можно найти выход из этого положения просто пригласив к сделке юристов и эксроу-посредников. Но мы ведь обсуждаем не реальную сферу, а криптографию. А как говорят сами криптографы в своих работах, для того, чтобы найти решение какого либо вопроса, нужно просто придумать полностью выходящее за рамки установленных норм решение. То есть это должно быть неординарное техническое решение.
Для получения такого решения корпорация пошла на консультацию к специалисту Силвио Микали, сотруднику MIT. Он посоветовался со своими хорошими коллегами Оде Голдрихом и Ави Виджерсоном. В результате этих переговоров был разработан новый протокол, который оказался настолько передовым, что для его функционирования даже не нужны компьютеры. Всё оказалось очень просто. Нужно просто большое количество разноцветных карандашей и бумажные листы. К тому же понадобится приличное количество шляп. А вот насколько просто и как это будет всё работать, рассмотрим в следующей статье.

