История появления критерия Келли
История появления критерия Келли
Как следует из самого названия, авторство принадлежит ученому из Техаса по имени Джон Ларри Келли младший. В 1956 году он вывел формулу для определения того, каким процентом своего капитала нужно рисковать в последовательности ставок с положительным ожидаемым значением, чтобы максимально увеличить прибыль. Критерий, который он явил свету, сегодня хорошо известен тем, кто делает ставки на спортивные мероприятия.
Вообще поиск оптимальной ставки появился еще в XVIII веке, когда было активным обсуждение санкт-петербургского парадокса, иллюстрирующего расхождение между оптимальным поведением участника рынка и его здравым смыслом. Еще тогда мнения существенно разнились. Для одних было важно максимально сократить риск потери всего депозита за конкретное количество сделок, совершенных в будущем. Другие же сторонники полагали, что это число сделок нужно использовать для получения максимально возможной прибыли. Иными словами, обе стороны считали, что нужно использовать свой депозит эффективно, то есть применять функцию полезности. Даниил Бернулли, математик из Швейцарии, применил ее для решения санкт-петербургского парадокса, но потерпел неудачу.
Спустя пару столетий к ней вернулся Келли, попытавшись использовать интересные свойства формулы в сфере коммуникаций, где он работал на тот момент. Через пять лет Бриман опубликовал свое исследование, в котором подробно рассмотрел эти данные. В это же время американский экономист Гарри Марковиц применил формулу к ценным бумагам. В 1962 году американский профессор математики Эдварт Торп описал критерий Келли в своей книге.
Таким образом, название критерия отсылает нас к человеку, который вспомнил о формуле и тем самым дал толчок к ее изучению в различных сферах. Однако распространение она получила благодаря совершенно другим людям, использовавшим ее на финансовых рынках.

Вообще поиск оптимальной ставки появился еще в XVIII веке, когда было активным обсуждение санкт-петербургского парадокса, иллюстрирующего расхождение между оптимальным поведением участника рынка и его здравым смыслом. Еще тогда мнения существенно разнились. Для одних было важно максимально сократить риск потери всего депозита за конкретное количество сделок, совершенных в будущем. Другие же сторонники полагали, что это число сделок нужно использовать для получения максимально возможной прибыли. Иными словами, обе стороны считали, что нужно использовать свой депозит эффективно, то есть применять функцию полезности. Даниил Бернулли, математик из Швейцарии, применил ее для решения санкт-петербургского парадокса, но потерпел неудачу.
Спустя пару столетий к ней вернулся Келли, попытавшись использовать интересные свойства формулы в сфере коммуникаций, где он работал на тот момент. Через пять лет Бриман опубликовал свое исследование, в котором подробно рассмотрел эти данные. В это же время американский экономист Гарри Марковиц применил формулу к ценным бумагам. В 1962 году американский профессор математики Эдварт Торп описал критерий Келли в своей книге.
Таким образом, название критерия отсылает нас к человеку, который вспомнил о формуле и тем самым дал толчок к ее изучению в различных сферах. Однако распространение она получила благодаря совершенно другим людям, использовавшим ее на финансовых рынках.

Правила расчета критерия Келли
Правила расчета критерия Келли
При использовании этой формулы капитал трейдера растет, а риск разорения становится меньше от сделки к сделке. Это чудодейственные свойства критерия Келли, который определяется несколькими способами. В специализированной литературе можно найти множество вариантов формулы, причем все они будут правильными. Если свести их все к общему виду, то получится следующая математическая фраза: Х = р – q/w.
Под знаком «р» здесь обозначается вероятность успешной сделки, под знаком «q» – риск потерять средства при неудачной сделке. Буквой «w» заменяют средний процент успеха. А «Х» – это та доля вашего капитала, которая превращается в ставку при открытии сделки. Она выражается в процентах, поэтому при значении 0,2 ставка сделки будет равна 20% от всего капитала.
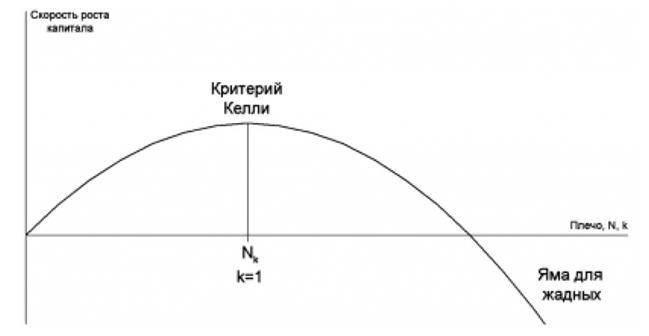
То, с какой скоростью будет расти капитал, напрямую зависит от выбранного кредитного плеча. Его увеличение влияет на линейный рост прибыли, но в то же самое время убыток пересчета становится больше в квадратичном размере. Отсюда следует вывод, что общая доходность растет медленнее, а после того, как достигнет некоторой оптимальной точки, падает и постепенно уходит в минус. Это дает объяснение тем случаям, когда трейдер уверен в своей стратегии, имеет хороший процент доходных сделок, но при увеличении плеча вдруг теряет весь свой капитал. Таким образ, существует оптимальный размер плеча, высчитанный по формуле Келли, при котором можно извлечь максимальную прибыль и выше которого нельзя подниматься, поскольку это приводит в так называемую яму для жадных, потерявших все свои средства.
Под знаком «р» здесь обозначается вероятность успешной сделки, под знаком «q» – риск потерять средства при неудачной сделке. Буквой «w» заменяют средний процент успеха. А «Х» – это та доля вашего капитала, которая превращается в ставку при открытии сделки. Она выражается в процентах, поэтому при значении 0,2 ставка сделки будет равна 20% от всего капитала.
То, с какой скоростью будет расти капитал, напрямую зависит от выбранного кредитного плеча. Его увеличение влияет на линейный рост прибыли, но в то же самое время убыток пересчета становится больше в квадратичном размере. Отсюда следует вывод, что общая доходность растет медленнее, а после того, как достигнет некоторой оптимальной точки, падает и постепенно уходит в минус. Это дает объяснение тем случаям, когда трейдер уверен в своей стратегии, имеет хороший процент доходных сделок, но при увеличении плеча вдруг теряет весь свой капитал. Таким образ, существует оптимальный размер плеча, высчитанный по формуле Келли, при котором можно извлечь максимальную прибыль и выше которого нельзя подниматься, поскольку это приводит в так называемую яму для жадных, потерявших все свои средства.

Как использовать критерий Келли в торговле?
Как использовать критерий Келли в торговле?
В первую очередь, необходимо проверить, дает ли используемая торговая система положительное математическое ожидание. Для этого нужно рассчитать процент успешных и убыточных сделок, причем размер результата тоже важен. 20 из 100 сделок могут дать +30%, а 10 из того же количества – целых +40%. Складываем процентные выражения доходности, умноженные на количество сделок, в которых они повторялись.
Пример. Если у вас было 10 сделок, давших результат +40%, 30 сделок, принесших +20%, а также 20 убыточных сделок с -30% и 30 с результатом -10%, то формула выглядит следующим образом:
0,4х10 + 0,2х30 – 0,3х20 – 0,1х30 = 1. Это значение больше нуля, а значит, математическое ожидание положительно. Если сумма меньше нуля либо равна ему, то стратегия приведет к полной потере капитала, несмотря на высокую волатильность. В данном случае четко выверенная система управления капиталом помочь не сможет.
Полученное значение нужно подставить в формулу ниже:
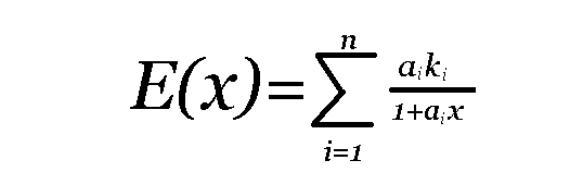
При этом существует единственно 0<f<-1/a1, при котором E(f)=0. Чтобы уравнение имело решение, необходимо подобрать такое значение «х», чтобы вся формула сводилась к нулю. Для этого можно использовать любую программу, берущую на себя заботы по управлению сложными математическими операциями.
По окончании вычислительных действий у вас останется значение, равное такому проценту капитала, которое может служить оптимальной ставкой. В том случае, если вы используете кредитное плечо, нужно привести результат к соотношению 1:1 с плечом.
Пример. Если у вас было 10 сделок, давших результат +40%, 30 сделок, принесших +20%, а также 20 убыточных сделок с -30% и 30 с результатом -10%, то формула выглядит следующим образом:
0,4х10 + 0,2х30 – 0,3х20 – 0,1х30 = 1. Это значение больше нуля, а значит, математическое ожидание положительно. Если сумма меньше нуля либо равна ему, то стратегия приведет к полной потере капитала, несмотря на высокую волатильность. В данном случае четко выверенная система управления капиталом помочь не сможет.
Полученное значение нужно подставить в формулу ниже:
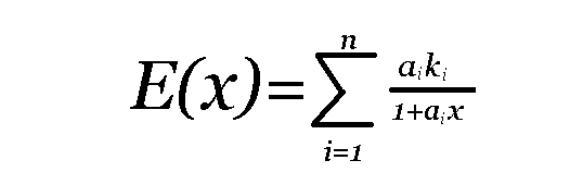
При этом существует единственно 0<f<-1/a1, при котором E(f)=0. Чтобы уравнение имело решение, необходимо подобрать такое значение «х», чтобы вся формула сводилась к нулю. Для этого можно использовать любую программу, берущую на себя заботы по управлению сложными математическими операциями.
По окончании вычислительных действий у вас останется значение, равное такому проценту капитала, которое может служить оптимальной ставкой. В том случае, если вы используете кредитное плечо, нужно привести результат к соотношению 1:1 с плечом.
Преимущества и недостатки применения критерия Келли
Преимущества и недостатки применения критерия Келли
Самый большой плюс, который можно найти в работе с данным критерием, – это высокий уровень защищенности капитала. Если использовать формулу, которую предложил американский ученый в прошлом веке, то риск потерять весь свой счет сводится практически к нулевому значению. Даже в том случае, если в торговле начнется черная полоса и целая серия крупных неудач, то потери все равно составят минимально возможный процент от всей суммы.
В качестве недостатков можно привести несколько аспектов, которые скорее являются особенностями, нежели очевидными минусами.
Первый из них – это обязательное наличие большого количества сделок. Только так можно быть уверенным в том, что расчеты верны, в противном же случае, если сделок немного, есть риск потерять свой капитал.
Второй нюанс касается удобства использования критерия. Значение, полученное в результате расчетов, актуально только для текущей сделки. Для последующих 5-10 сделок изменения не будут критичными, но дальнейшая торговля потребует пересчитать значения.
Третий недостаток – сложность математической формулы, которую необходимо применять вручную. Это крайне неудобно для тех, кто торгует внутри одного дня.
Четвертая особенность говорит скорее против критерия Келли. Речь идет о том, что он не учитывает неравномерный характер чередования успешных и неудачных сделок. Таким образом, он не может рассчитать значение с учетом длительной серии убытков.

В качестве недостатков можно привести несколько аспектов, которые скорее являются особенностями, нежели очевидными минусами.
Первый из них – это обязательное наличие большого количества сделок. Только так можно быть уверенным в том, что расчеты верны, в противном же случае, если сделок немного, есть риск потерять свой капитал.
Второй нюанс касается удобства использования критерия. Значение, полученное в результате расчетов, актуально только для текущей сделки. Для последующих 5-10 сделок изменения не будут критичными, но дальнейшая торговля потребует пересчитать значения.
Третий недостаток – сложность математической формулы, которую необходимо применять вручную. Это крайне неудобно для тех, кто торгует внутри одного дня.
Четвертая особенность говорит скорее против критерия Келли. Речь идет о том, что он не учитывает неравномерный характер чередования успешных и неудачных сделок. Таким образом, он не может рассчитать значение с учетом длительной серии убытков.

Выводы
Выводы
Работа с критерием Келли требует глубоких знаний в области математики, но для тех, кто готов к трудностям, он открывает возможности для достижения поставленной цели за определенное количество попыток, дает наглядное представление о том, как будет меняться размер капитала, а также обнаруживает другие полезные свойства, необходимые при торговле.

ПАРИТЕТ НАУКА ВЗВЕШЕННЫХ ИНВЕСТИЦИЙ


ПАРИТЕТ НАУКА ВЗВЕШЕННЫХ ИНВЕСТИЦИЙ

Торговые роботы и стратегии. Обучение трейдингу.

paritet.group

Интереснейшее инвестиционное предложение
Безграничные перспективы или как начать с нуля +Конкурс на $1000 в MTHUB
Продолжение обзора
Прохождение квалификационного теста MTHUB (доверительное управление)
Теория
Обсуждение/общение. Вопросы/ответы
ЗАЙТИ В ГОСТИ К РОБИНУ

paritet.group
Интереснейшее инвестиционное предложение
Безграничные перспективы или как начать с нуля +Конкурс на $1000 в MTHUB
Продолжение обзора
Прохождение квалификационного теста MTHUB (доверительное управление)
Теория
Обсуждение/общение. Вопросы/ответы
ЗАЙТИ В ГОСТИ К РОБИНУ
